A GPU Parallel Algorithm for Computing Morse-Smale Complexes
Varshini Subhash, Karran Pandey and Vijay Natarajan.IEEE Transactions on Visualization and Computer Graphics, 29 (9), 2023, 3873-3887.
Abstract
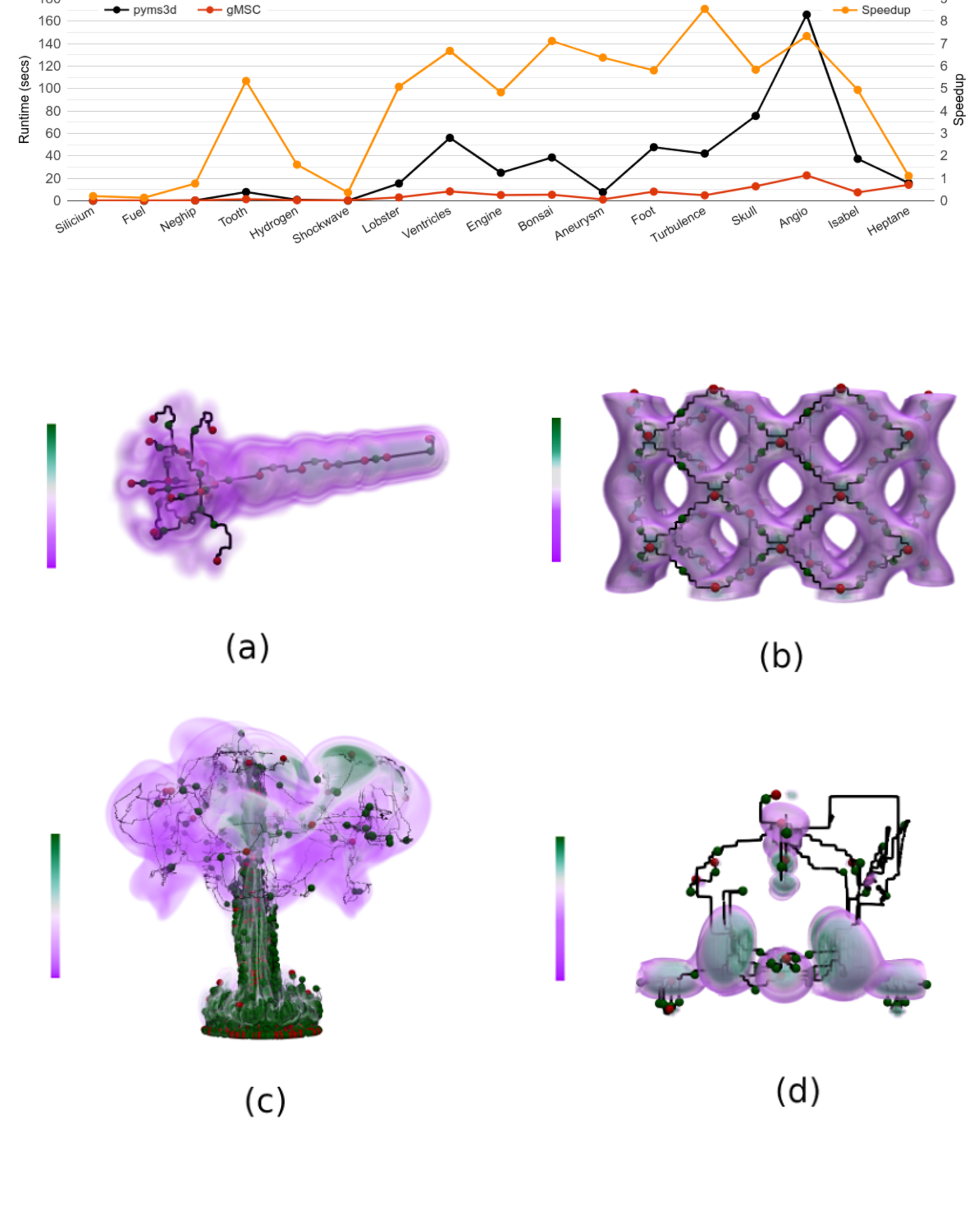
The Morse-Smale complex is a well studied topological structure that represents the gradient flow behavior between critical points of a scalar function. It supports multi-scale topological analysis and visualization of feature-rich scientific data. Several parallel algorithms have been proposed towards the fast computation of the 3D Morse-Smale complex. Its computation continues to pose significant algorithmic challenges. In particular, the non-trivial structure of the connections between the saddle critical points are not amenable to parallel computation. This paper describes a fine grained parallel algorithm for computing the Morse-Smale complex and a GPU implementation (gMSC). The algorithm first determines the saddle-saddle reachability via a transformation into a sequence of vector operations, and next computes the paths between saddles by transforming it into a sequence of matrix operations. Computational experiments show that the method achieves up to 8.6× speedup over pyms3d and 6× speedup over TTK, the current shared memory implementations. The paper also presents a comprehensive experimental analysis of different steps of the algorithm and reports on their contribution towards runtime performance. Finally, it introduces a CPU based data parallel algorithm for simplifying the Morse-Smale complex via iterative critical point pair cancellation.[PDF]
Supplementary Material:
- Supplementary material for "A GPU Parallel Algorithm for Computing Morse-Smale Complexes" (Download)