Visualization of biomolecular channels and cavities
People involved: Talha Bin Masood and Raghavendra G.S.
Fundamentally all biological processes are molecular in nature. So, it is essential to understand biomolecules
and their interactions to gain better insight into living systems. Proteins are constituted of chains of small building
blocks called amino acids. These chains of amino acids fold in 3D space to define structure of a protein. It is
known that structure of biomolecules plays an important role in defining its function. Biomolecular structures
contain complex features such as pockets and protrusions on the surface, internal cavities and voids, channel
and tunnel like structures connecting external surface to functional sites buried deep inside the molecule.
Analysis of these features is very important for understanding of structure-function relationships, engineering
new proteins with required functional properties, or designing inhibitors for existing proteins.
Proteins are often represented in space-fill model as a union of balls, where each ball corresponds to an atom (See Figure 1).
This model is ideal for application of geometric and topological techniques for detailed analysis. For example,
geometric algorithms have been developed for extraction of molecular surface which is extremely important
in the study of any protein. Similarly, for accurate measurement of molecular volumes, identification and
characterization of empty space within a molecule, methods from computation geometry and topology are
applied. This project is a contribution to this area of research with special focus on integrated geometric and
topological methods for visual analysis of cavities and channels in biomolecules.
With increasing availability of structures of large proteins and protein complexes at atomic detail through
advancements in the field of crystallography, there is a need of designing faster and more space efficient algorithms
for their analysis. Another driver for the need of efficient geometric algorithms is the availability of larger
molecular dynamics trajectories, which are essentially time varying molecular structures. Designing algorithms
to address these challenges is the second major focus of this project.
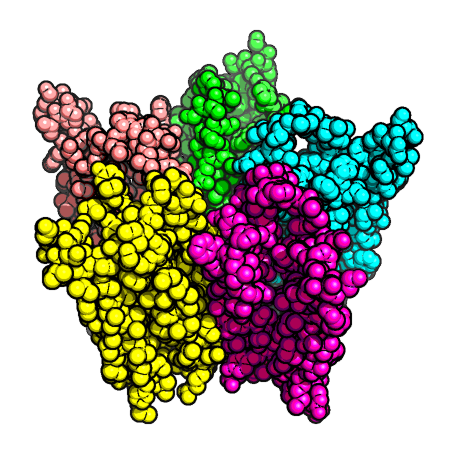
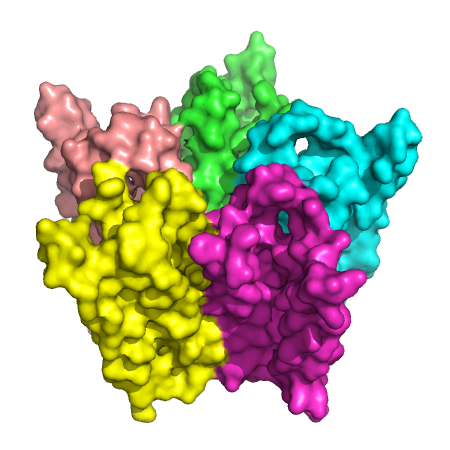
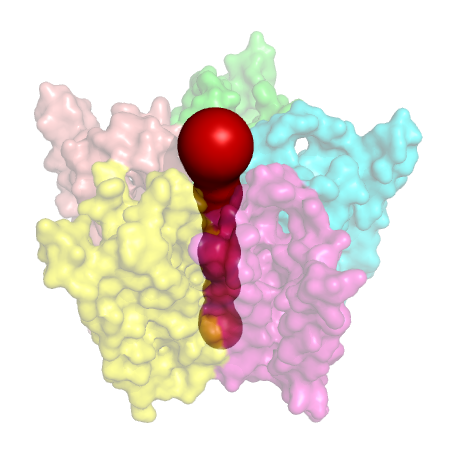 Figure 1. ACH receptor transmembrane protein (PDB id: 1OED). (Left) The space-fill model.
(Middle) The molecular surface. (Right) The central transmembrane pore through this protein.
Figure 1. ACH receptor transmembrane protein (PDB id: 1OED). (Left) The space-fill model.
(Middle) The molecular surface. (Right) The central transmembrane pore through this protein.
In the first part, we describe two methods: one for extraction and visualization of biomolecular
channels, and the other for extraction of cavities in uncertain data. We also describe the two software tools based
on the proposed methods targeted at the end-user, the biologists. These two web server tools publicly available
for use are called ChExVis and RobustCavities. In the second part, we describe efficient parallel
algorithms for two geometric structures widely used in the study of biomolecules. One of the structures we
discuss is discrete Voronoi diagram which finds applications in channel visualization, while the other structure
is alpha complex which is extremely useful in studying geometric and topological properties of biomolecules.
Extraction and visualization of channels
A channel is a pathway through empty space within the molecule. Understanding channels, that lead to active
sites or traverse the molecule, is important in the study of molecular functions such as ion, ligand, and small
molecule transport. Efficient methods for extracting, storing, and analysing protein channels are required to
support such studies. We develop an integrated framework that supports computation of the channels, interactive exploration of their structure, and detailed visual analysis of their properties [1]. Key contributions are
summarized below:
-
We describe a method for extraction of channels in biomolecules based on a representation of the molecule
using the alpha complex. This is exploited to capture all geometrically feasible channels in a concise
representation called channel network that supports querying for specific channels. The extracted channels
are represented as a set of connected tetrahedra.
- Novel methods are developed to automatically identify important channels within the network and rank
them based on their significance.
- The channel extraction method was compared with the existing software tools. The quality of the results
was observed to be better than or comparable to other tools – Mole, Caver, MolAxis, and PoreWalker.
- Novel visualization methods are proposed to facilitate detailed study of the extracted channels. Figure 2
shows visualization of potassium channel in a transmembrane protein.
- The integrated channel extraction and visualization framework was successfully used to study multiple
transmembrane pores and channels leading to active sites.
- These methods are implemented as a web server called ChExVis which is available for public use.

Figure 2. Transmembrane pore identified in PDB structure 1K4C using our channel extraction method. The 3D view of the channel is shown on the left. Conservation and hydrophobicity profiles are shown using a blue
to red color map in the middle. Four different 2D box representations of the channel are shown on the right.
From left to right, boxes are labelled by amino acid type, atom type, structure and chemical properties of the
lining atoms.
Extraction of robust voids and pockets in proteins
A cavity in a protein molecule refers to both voids (without openings) and pockets (with openings). These cavities play a key role in determining the stability and function of proteins. The existing methods for detection of cavities take protein structures determined from x-ray crystallography data or other lower resolution data as input. These methods are sensitive to inaccuracies that are inherent in the crystallographic measurements. While the measurements may guarantee high resolution, it is
important to note that even small inaccuracies may cause a difference in the reported
number of cavities. Inaccuracies may also arise due to fundamental limitations such
as the notion of radii of atoms, which is determined empirically. Presence of such inaccuracies may result in a cavity detection
method to report two distinct but large cavities in place of one, or report very small
volume cavities. Figure 3 illustrates the problem as it occurs in a lyzosyme protein. Key contributions of this work [2] include:
-
We develop an interactive method to compute robust cavities in proteins where the goal is to enable the user to reduce, if not completely eliminate, the inaccuracies mentioned earlier.
- We provide a novel definition for robustness in the presence of inaccuracies in the measured radii.
- We propose a method for computing robust and stable cavities in proteins.
This is accomplished through the use of a simple and succinct structure called the
alpha complex to represent protein molecules. In order to identify the set of cavities that are stable with respect to small
perturbations in the atom radii, our method symbolically modifies the radii of a select set of atoms by systematically processing and modifying the filtration. The method is efficient
in terms of running time performance and also supports the elimination of very small
or insignificant voids as measured by the notion of topological persistence.
- We also develop software to visualize the stable cavities together with the molecule,
and to calculate cavity volumes and surface areas. This software provides an interactive framework that a biologist can use to decide which cavities are more relevant
and what mutations to perform.
- We use this software to demonstrate the applicability of the notion of
robust voids and pockets and apply it to detect potential channels and pockets in
several proteins.
- These methods are also implemented as a web server called RobustCavities which is available for public use.


Figure 3. The two cavities
that appear very near to each other in a lyzozyme protein (200L) may be a single cavity. The solid
surface represents cavities while the protein is shown as cartoon to provide context.
Connecting cavities in biomolecules
The tools and techniques developed for extraction of cavities in molecules are sensitive to uncertainties in atomic
position and radii (Refer to Figure 4 for an example). We study the problem of cavity extraction in biomolecules
while taking into account such uncertainties [3]. We propose a simple and direct approach to address this
problem, where the user examines the cavities and identifies artifacts or undesirable disconnections. The user
interacts with the multiple linked views provided by the visualization and specifies a pair of cavities to be connected. Our cavity connection algorithm efficiently and automatically computes an optimal conduit between
the cavities. Key contributions include:
- A simple, explicit, and flexible method for extracting cavities in biomolecules from uncertain data with
guaranteed bounds on the perturbation required.
- Efficient algorithms to compute a conduit between user selected cavities that satisfies well defined optimality criteria.
- Interactive visualization of cavities in a molecule with multiple linked views that facilitates identification
of disconnected cavities.
- Case studies that demonstrate the benefits of the cavity connection based method.
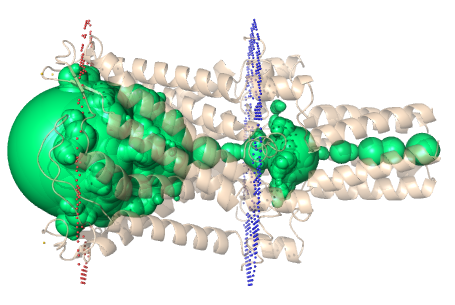
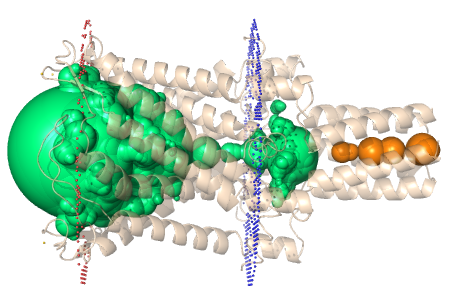
Figure 4. (Left) Biologically relevant transmembrane pore in the protein (PDB id: 2OAR) is identified as two disconnected cavities using existing methods. (Right) Using our approach, we find the best path to connect the two
cavities and correctly identify the biologically significant pore.
Parallel computation of discrete Voronoi diagram
Voronoi diagram, a partitioning of space based proximity to input point sites, is one of the most widely studied
structure in computational geometry. In the context of structural biology, it plays a key role in the identification
of channels in proteins, computation of molecular surfaces, determining depth of binding sites, etc. Voronoi
diagram also finds applications in computer graphics, image processing, mesh processing, robot navigation, and
for data analysis in several scientific and engineering disciplines. In most cases, Voronoi diagrams are computed
for the continuous case where the space of interest is 2D or 3D Euclidean space and the input set of sites is
finite. Discrete Voronoi diagram however requires the computation of regions on a discrete grid of finite pixels,
with seed points being some of the pixels themselves. Jump Flooding can be used to generate discrete Voronoi
diagrams. We introduce a variant of JFA, called Facet-JFA, wherein only the pixels that are located near the
Voronoi region boundaries are processed, thus immensely reducing the total amount of work done by the
algorithm [4]. The key results are summarized below:
- A novel variant of JFA, called Facet-JFA. This strategy enables both space optimization and better running times in practice. We observed upto 10x speed-up over JFA using Facet-JFA.
- The algorithm uses an intrinsic quad tree-based approach and requires only log n steps to compute the
Voronoi diagram for an n x n grid of pixels.
- A GPU accelerated technique for extraction of the channel network in biomolecules in two and three
dimensions which uses Facet-JFA (See Figure 5).
- The proposed method allows extraction of channels at real-time interactive rates and is thus suited for
visual analysis of static and dynamic channel structures in Molecular Dynamics (MD) simulation trajectories.


Figure 5. (Left) A transmembrane protein (PDB id: 1OED). (Right) The channel network extracted using Facet-JFA.
Parallel computation of alpha complex
Alpha complex, a subset of Delaunay triangulation, has been extensively used as a tool in the study of biomolecular structures. It is crucial for the accurate computation of geometric properties of biomolecule like volume
and surface area. We propose an algorithm that avoids the expensive Delaunay triangulation computation and
instead directly computes the alpha complex for biomolecules (See Figure 6). The key contributions are summarized below:
- A new characterization of the alpha complex – a set of conditions necessary and sufficient for a simplex
to be a part of the alpha complex.
- A new algorithm for computing the alpha complex of a set of weighted points in 3D. The algorithm identifies simplices of the alpha complex in decreasing order of dimension without computing the complete
weighted Delaunay triangulation.
- An efficient CUDA based parallel implementation of this algorithm for biomolecular data that can compute the alpha complex for a 10 million point dataset in approximately 10 seconds.
- A proof of correctness of the algorithm and comprehensive experimental validation to demonstrate that
it outperforms existing methods.

Figure 6. Illustration of the proposed algorithm in 2D. (a) The set of disks grown by the
parameter alpha. (b) First, compute the set of edges whose ortho-size is smaller than alpha (red). The triangles
that satisfy this condition are also computed but they are not shown here. (c) Next, identify
the triangles that satisfy the Delaunay condition (red). (d) For the edges not incident on triangles identified till now, check if they satisfy Delaunay condition. (e) Only one edge survives
this check and thus belongs to the alpha complex. (f) The alpha complex is obtained as the union of triangles, edges and vertices identified as valid alpha simplices.
Publications
- Talha Bin Masood, Sankaran Sandhya, Nagasuma Chandra and Vijay Natarajan.
ChExVis: a tool for molecular channel extraction and visualization.
- Raghavendra Sridharamurthy, Talha Bin Masood, Harish Doraiswamy, Siddharth Patel, Raghavan Varadarajan and Vijay Natarajan.
Extraction of robust voids and pockets in proteins.
- Talha Bin Masood and Vijay Natarajan.
An integrated geometric and topological approach to connecting cavities in biomolecules.
- Talha Bin Masood, Hari Krishna Malladi and Vijay Natarajan.
Facet-JFA: Faster computation of discrete Voronoi diagrams.
Software
-
ChExVis
A web server for molecular Channel Extraction and Visualization.
-
RobustCavities
Web portal for a software which computes cavities in proteins robustly taking into account uncertainties in the atomic radii.
Contact
Contact: talha [at] iisc [dot] ac [dot] in.










