Feature Preserving Mesh Simplification
People involved: Dilip ThomasSeveral applications generate high resolution meshes and often these meshes have to be simplified for faster computations on the mesh. Many of these meshes contain interesting features that should be preserved during simplification. We consider two specific simplification problems that require feature preservation and develop edge contraction based simplification schemes that ensure feature preservation.
Topology Preserving Simplification of Meshes with Embedded Structures
Many meshes contain interesting substructures of lower dimensions embedded within the mesh. The topology of such embedded structures is often important. For instance, in a mesh that contains two distinct regions, the boundary separating the two regions could be an embedded structure whose topology needs to be preserved while simplifying the mesh.We show that evaluating a set of local conditions, called link conditions, guarantees topology preservation of the mesh together with its embedded structures. We also show that these conditions are necessary for topology preservation in most cases. Our simplification scheme generates a coarse mesh with good quality mesh elements and also approximates the scalar field defined on the mesh.
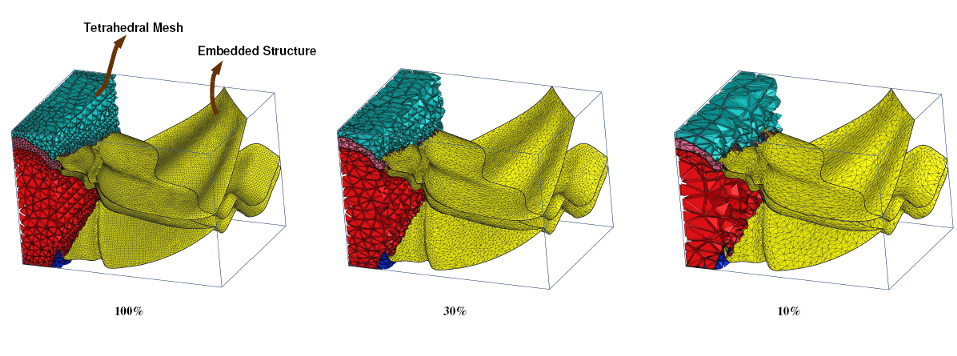Cutaway view of a tetrahedral mesh modeling different soil types before and after simplification. The topology of regions containing different soil types is important for earthquake prediction, oil exploration, and mining. The boundary between different soil types is treated as an embedded structure (shown in yellow). Topology of the mesh and the embedded structure is preserved during simplification
Adaptive Mesh Simplification for Faster Diffuse Optical Tomography Image Reconstruction
The use of near-infrared Diffuse Optical Tomography (DOT) for breast cancer imaging is an area of active research in the medical community. High-resolution images from traditional imaging modalities like MRI are used to construct meshes that model human breast. Finite Element based image reconstruction technique is used to estimate the optical properties of the different regions of the breast which help to detect breast cancer. We identify the spatial region that has low sensitivity to DOT measurement and adaptively simplify the mesh. We show that our simplification scheme introduces only negligible error in reconstruction, but speeds up computations considerably.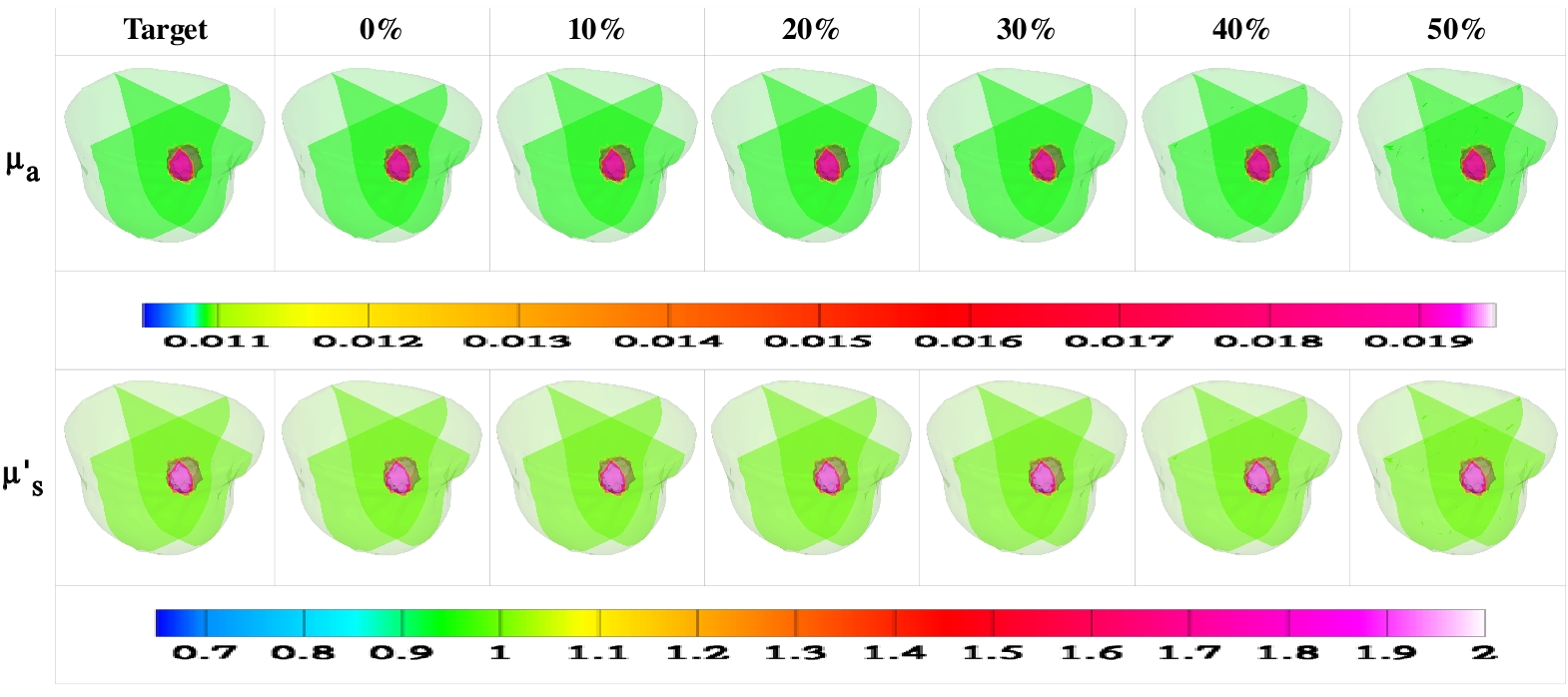
Figure above shows a visual representation of the optical properties of a breast model. The region in purple indicates presence of a tumour. The expected values of the optical properties are given by the target mesh. The actual values computed at different simplification levels are shown. As can be seen from the figure, there is no significant change in the optical properties computed even after 50% simplification but results in 3 times speed up in computation time.
Publications
- Dilip Mathew Thomas, Vijay Natarajan, and Georges-Pierre Bonneau.
Link conditions for simplifying meshes with embedded structures. - Dilip Mathew Thomas, Phaneendra K. Yalavarthy, Deepak Karkala, and Vijay Natarajan.
Mesh simplification based on edge collapsing could improve computational efficiency in near infrared optical tomographic imaging.