Analyzing time-varying scalar fields using piecewise-linear Morse-Cerf theory
Amritendu Dhar, Apratim Chakraborty, and Vijay Natarajan.IEEE VIS 2025: Proc. IEEE Conference on Visualization (short papers), 2025, In Press.
Abstract
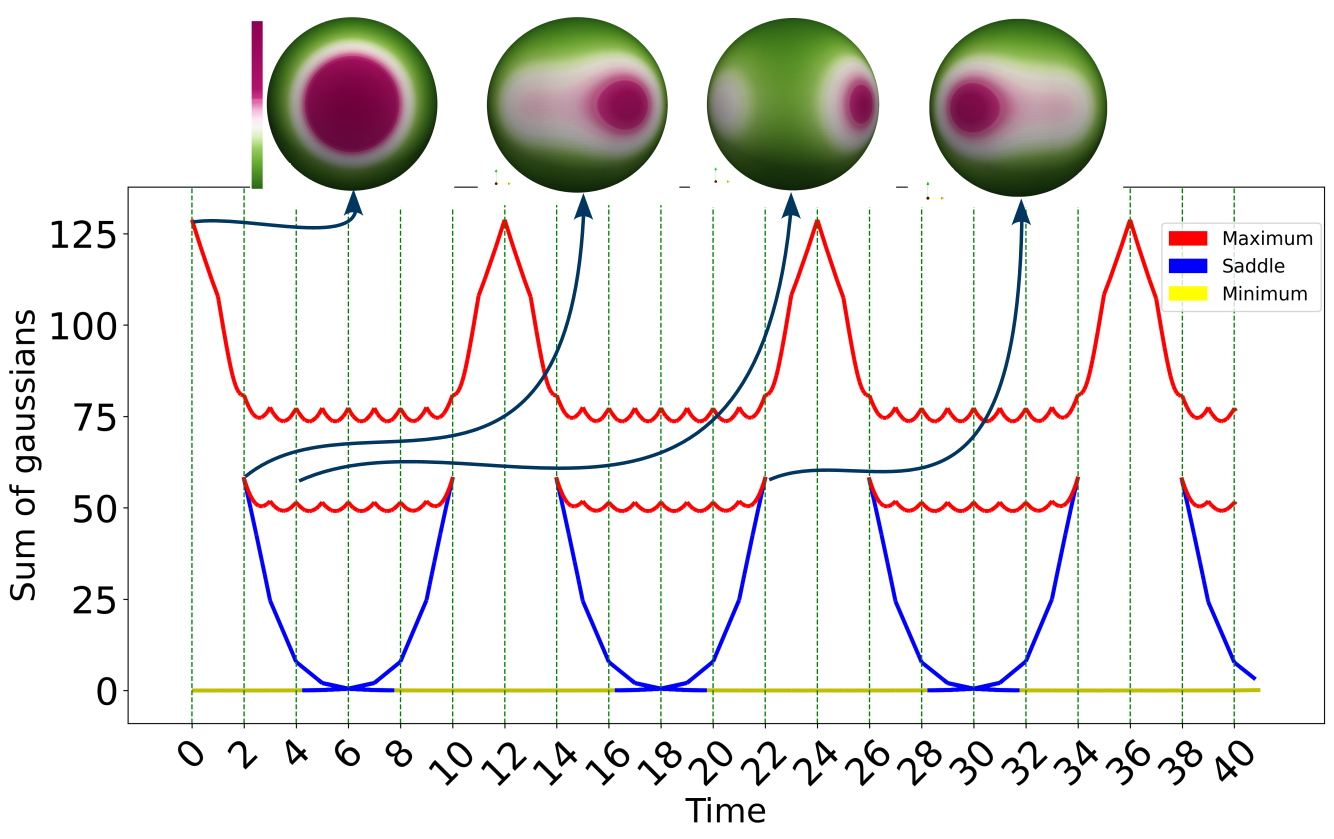
Morse-Cerf theory considers a one-parameter family of smooth functions defined on a manifold and studies the evolution of their critical points with the parameter. This paper presents an adaptation of Morse-Cerf theory to a family of piecewise-linear (PL) functions. The vertex diagram and Cerf diagram are introduced as representations of the evolution of critical points of the PL function. The characterization of a crossing in the vertex diagram based on the homology of the lower links of vertices leads to the definition of a topological descriptor for time-varying scalar fields. An algorithm for computing the Cerf diagram and a measure for comparing two Cerf diagrams are also described together with experimental results on time-varying scalar fields.[PDF]
Supplementary Material:
- Supplementary material for "Analyzing time-varying scalar fields using piecewise-linear Morse-Cerf theory" (Download)