On-Demand Augmentation of Contour Trees

Mohit Sharma and Vijay Natarajan.
ICVGIP 2018: 31:1-31:8

Abstract

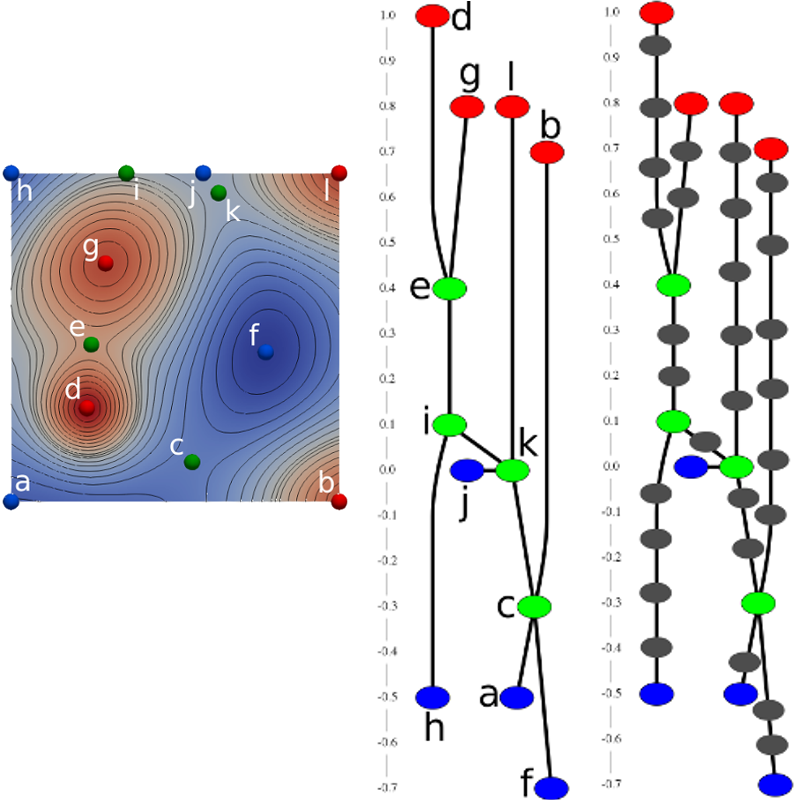
The contour tree represents the topology of level sets of a scalar function. Nodes of the tree correspond to critical level sets and arcs of the tree represent a collection of topologically equivalent level sets connecting two critical level sets. The augmented contour tree contains degree-2 nodes on the arcs that represent regular level sets. The degree-2 nodes correspond to regular points of the scalar function and other critical points that do not affect the number of level set components. The augmented contour tree is significantly larger in size and requires more effort to compute when compared to the contour tree. Applications of the contour tree to data exploration and visualization require the augmented contour tree. Current approaches propose algorithms to compute the contour tree and the augmented contour tree from scratch. Precomputing and storing the large augmented contour tree will not be necessary if the contour tree can be augmented on-demand. This paper poses the problem of computing the augmented contour tree given a contour tree as input. Computational experiments demonstrate that the on-demand augmentation can be computed fast while resulting in good memory savings.

[PDF]