A brief primer on Morse-Smale complexes
What is a Scalar Field?
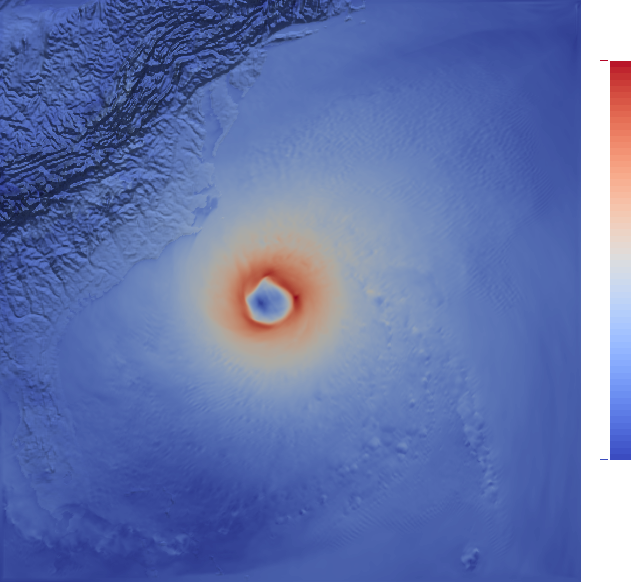
A scalar field is a numerical measure of an interesting quantity over a domain of study. The figure shows the wind speed scalar field computed from a simulation of the hurricane Isabel that struck the coast of Florida, USA, in September of 2003. Here, red colors depict high speeds and blue low speeds. A typical feature of a hurricane is that the wind speeds are very low at the eye with very high speeds around it. The eye in this image, which is clearly visually perceptible, is often a feature of interest.
What is the Morse-Smale complex?
The Morse-Smale complex is a topological data structure that is constructed based on the gradient of a given scalar field. Informally, the gradient at any point of the domain captures the direction along which the change of the scalar field is maximized.
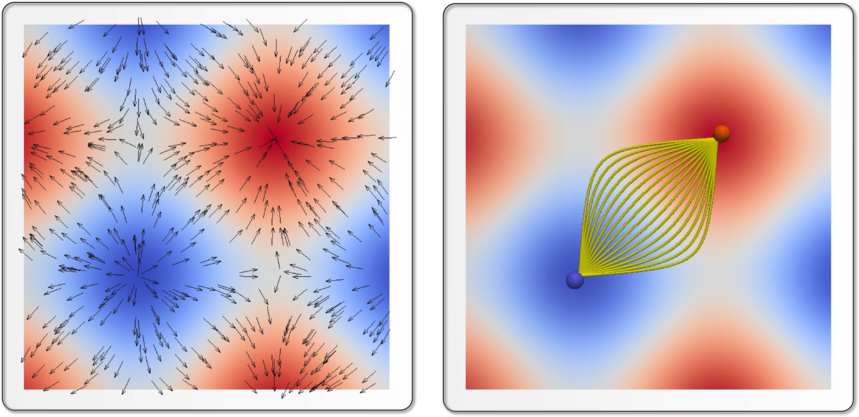
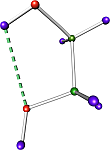
The image on the left shows an example of gradients for the scalar field computed by the analytic function sin(x) + sin(y) . Integral lines passing through a given point are constructed by integrating along and against the gradient. Integral lines originate and terminate at critical points where the gradients vanish. The Morse-Smale complex is defined as the partition of the domain into cells whose integral lines share a common origin and terminal. The image on the right shows an example of a Morse-Smale cell formed by a set of integral lines that share a common origin and terminal.
What is it used for?
Morse-Smale complexes are employed in several data processing and visualization tasks. The following lists a few tasks
- Feature identification extraction and tracking
- Topology/Homology computations/simplification
- Scientific data visualization
- Data segmentation and analysis