Morse-Smale complexes: Computation and applications.

Nithin Shivashankar

Abstract

In recent decades, scientific data has become available in increasing sizes and precision. Therefore techniques to analyze and summarize the ever increasing datasets are of vital importance. A common form of scientific data, resulting from simulations as well as observational sciences, is in the form of scalar-valued function on domains of interest. The Morse-Smale complex is a topological data-structure used to analyze and summarize the gradient behavior of such scalar functions. This thesis deals with efficient parallel algorithms to compute the Morse-Smale complex as well as its application to datasets arising from cosmological sciences as well as structural biology.

The first part of the thesis discusses the contributions towards efficient com- putation of the Morse-Smale complex of scalar functions defined on two and three dimensional datasets. In two dimensions, parallel computation is made possible via a paralleizable discrete gradient computation algorithm. This algorithm is extended to work efficiently in three dimensions also. We also describe efficient algorithms that synergistically leverage modern GPUs and multi-core CPUs to traverse the gradient field needed for determining the structure and geometry of the Morse-Smale complex. We conclude this part with theoretical contributions pertaining to Morse-Smale complex simplification.

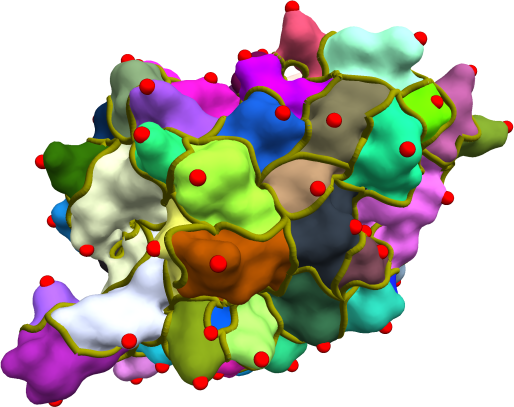
The second part of the thesis explores two applications of the Morse-Smale complex. The first is an application of the 3-dimensional hierarchical Morse- Smale complex to interactively explore the filamentary structure of the cosmic web. The second is an application of the Morse-Smale complex for analysis of shapes of molecular surfaces. Here, we employ the Morse-Smale complex to determine alignments between the surfaces of molecules having similar surface architecture.

[PDF]