ReCon is a library that computes the Reeb graph of a scalar function defined over a simplicial complex. It supports 2D, 3D, and higher dimensional meshes as input. Both Java and C++ versions of the library are available for download. The readme file provides details regarding the file formats that are supported. The library implements the algorithm described in [1].

The Recon algorithm:
This algorithm maximally leverages the efficient algorithms available to compute the loop-free version of the Reeb graph. It partitions the input into subsets whose Reeb graph do not contain any loops and merges the loop-free graphs in linear time to construct the Reeb graph of the input. The algorithm has a worst case running time of O(v log v + sn), which is close to the lower bound Ω(v log v + n). Here v is the number of vertices, n is the number of triangles, and s is the number of saddles in the input. In practice, the running times scale linearly with the number of triangles. The algorithm is up to two orders of magnitude faster than existing generic algorithms that support higher dimensional and non-manifold data. The performance is on par with algorithms that are catered to restricted classes of input. The algorithm is also amenable to handle large data that do not fit in memory.

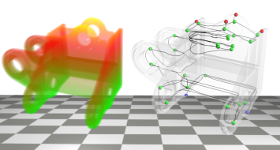
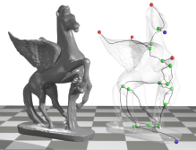
Reeb graph of the height function defined on a few objects. Reeb graph tracks the topology of level sets.

Source code on GitHub

References

1. Harish Doraiswamy and Vijay Natarajan.
   Computing Reeb graphs as a union of contour trees.
   IEEE Transactions on Visualization and Computer Graphics, 19 (2), 2013, 249-262.