Bivariate Data Visualization

People involved: Mohit Sharma, Dhruv Meduri

Understanding complex phenomena in diverse scientific and engineering disciplines often relies on decoding the relationship among real-valued or scalar fields that are measured or computed over a spatial domain. We explore the relationships between paired scalar fields, resulting in contributions that may be categorized under computation, generalization, applicability, and simplification. Specifically, we present methods for efficient computation and exploration of topological structures of bivariate fields, extend univariate concepts to the bivariate fields, and apply these structures across various applications.

Motivation

In many real-world scenarios across diverse scientific and engineering disciplines, phenomena depend on the intricate interplay between multiple fields. Figure 1 illustrates the temperature and salinity distribution over the Bay of Bengal. A water mass can be defined by a temperature-salinity (T-S) curve, and numerous studies analyze the dynamics of water masses with unique temperature and salinity distributions, either by plotting T-S diagrams or through side-by-side analysis of the two fields.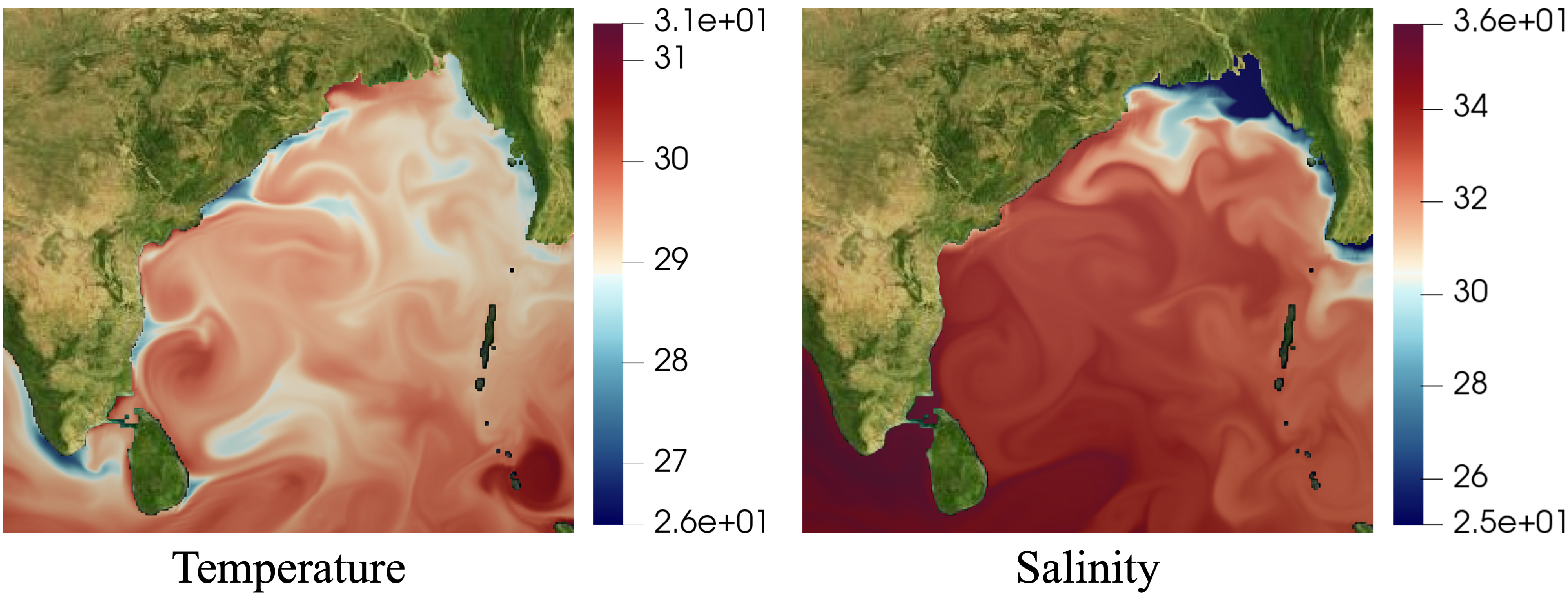




Figure 1: Surface temperature and salinity distribution over the Bay of Bengal on July 13, 2019. The two fields together are used to identify water masses.

In certain applications, derived fields complement the existing scalar field. In Figure 2 (left), different parts of a tooth are highlighted through isosurfaces extracted from the CT scalar field. Identifying interesting isovalues typically requires techniques like the contour spectrum or methods based on histograms or statistics derived from the scalar field. Bivariate field analysis, however, enables the extraction of interesting surfaces without explicitly identifying isovalues. Given the usefulness of gradient magnitude in designing multidimensional transfer functions for volume rendering, gradient magnitude is used as the second field to generate a continuous bivariate histogram (also known as a “continuous scatterplot”), shown in Figure 2 (right). The distinct parabolic curves are selected to highlight different parts of the tooth as fiber surfaces. Notably, the univariate analysis on the left cannot differentiate between the blue and yellow parts, due to the overlapping isovalue ranges of the CT field. Introducing a second axis (gradient magnitude) helps separate these parts in the bivariate range space.




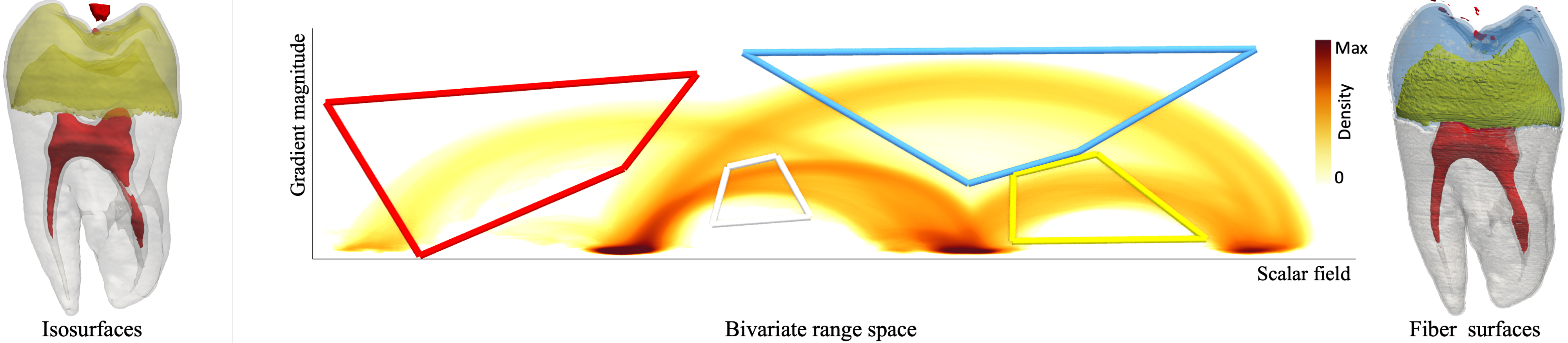
Figure 2: (Left) Parts of tooth highlighted by extracting isosurfaces: red (60), white (127.5) and yellow (200). (Right) The selected polygons in the bivariate range space help extract the parts captured by the parabolic curves. The blue and yellow parts are separated by introducing the gradient magnitude axis.

These analyses motivate the need to explore multivariate data in static and time-varying settings.

Objective and contributions

Our focus is confined to bivariate fields and deals with different aspects like,

• Computation. Enhancing the computation of existing bivariate structures.
• Generalization. Generalizing the univariate concepts to bivariate.
• Applicability. Leveraging bivariate constructs to study different applications.
• Simplification. Simplifying bivariate structures with respect to noise and clutter.

We make the following broad contributions.

• Jacobi set driven flexible fiber surface computation [1]: An output-sensitive method, enabling the flexible computation of fiber surface components, similar to flexible isosurfaces.
• Static bivariate fields analysis [2, 3]: Domain and range-driven CSP-based operators to study the relationship between the individual fields.
• Time-varying bivariate fields analysis: A track-based representation to study the evolution of bivariate features over time.
• Jacobi set Simplification [4]: A robustness-based method for Jacobi set simplification when one of the two fields represents time.

Jacobi set driven flexible fiber surface computation [1]

Fiber surfaces play a crucial role in visualizing significant bivariate values within the spatial domain. While existing methods for computing fiber surfaces use exhaustive search across the entire domain, we introduce a Jacobi set based output-sensitive approach. The approach yields the following significant contributions,

• An output-sensitive algorithm for fiber surface computation in tetrahedral meshes using the Jacobi set.
• An approach for flexible computation of individual fiber surface components.
• Interactive guided exploration of fiber surfaces within the vicinity of Jacobi edges.

Static bivariate field analysis [2,3]

We introduce methods for analyzing static bivariate fields, relying on continuous scatterplots (CSPs) and fiber surfaces. We demonstrate the effectiveness of these techniques using electronic transition datasets, which have been developed and interpreted in collaboration with theoretical chemists. The approaches provide valuable insights into electronic transition bivariate fields, addressing specific application questions. Key contributions include,

• A CSP lens operator that enables queries on the range space based on application-specific characteristics.
• A control polygon selection process that is directed by the CSP lens operator and helps in the extraction of fiber surfaces of interest.
• A domain segmentation driven CSP peeling operator that enables exploration of the bivariate field.
• A visual analysis pipeline that utilizes the two operators independently or conjointly.
• A quantification of CSPs to support visual analysis.
• Case studies on two molecular systems that demonstrate the utility and effectiveness of the pipeline in supporting the study of electronic transitions.

Time-varying bivariate field analysis

Dynamical phenomena are often represented as time-varying multivariate fields. While tracking graphs offer a static view of univariate field evolution, we focus on time-varying bivariate fields. We introduce a track-based representation that effectively captures the evolution of bivariate features, such as atoms in electronic transitions, over time. The significant contributions of this work include,

• An image moment-based method for visualizing and exploring the similarity and dissimilarity between CSPs.
• A new 4D representation of a time-varying bivariate field based on shape analysis of CSPs, and its visual presentation via a PCA plot.
• A visual analysis pipeline that employs the above methods to support the exploration of time-varying bivariate fields.
• Case studies that demonstrate the applicability and effectiveness of the visual analysis pipeline towards the study of excited-state dynamics in two molecular systems.

Jacobi Set Simplification for Tracking Topological Features in Time-Varying Scalar Fields [4]

The Jacobi set is a bivariate analog of critical points and may correspond to features of interest. For time-varying fields, where one scalar field represents time, the Jacobi set reflects temporal tracks of critical points. However, the complexity of the Jacobi set in bivariate or time-varying scalar fields often leads to cluttered visualizations. We address this by simplifying the Jacobi set using a stability measure called robustness, originally developed for vector fields, which captures the structural stability of critical points. Key contributions are,

• A robustness-based Jacobi set simplification algorithm for time-varying scalar fields,
• A mathematical analysis supporting the algorithm that guarantees the existence of a corresponding simplified vector field, and
• An implementation of the method for 2D time-varying scalar fields.

Publications

1. Mohit Sharma and Vijay Natarajan.
   Jacobi Set Driven Search for Flexible Fiber Surface Extraction
   
2. Mohit Sharma, Talha Bin Masood, Signe S. Thygesen, Mathieu Linares, Ingrid Hotz and Vijay Natarajan.
   Segmentation Driven Peeling for Visual Analysis of Electronic Transitions
   
3. Mohit Sharma, Talha Bin Masood, Signe S. Thygesen, Mathieu Linares, Ingrid Hotz and Vijay Natarajan.
   Continuous Scatterplot Operators for Bivariate Analysis and Study of Electronic Transitions
   
4. Dhruv Meduri, Mohit Sharma and Vijay Natarajan.
   Jacobi Set Simplification for Tracking Topological Features in Time-Varying Scalar Fields
   

Contact

mohitsharma [at] iisc [dot] ac [dot] in.