Comparative Analysis of Topological Structures for Visualization

People involved: Raghavendra G.S

Measuring scientific processes result in a set of scalar functions (scalar fields) which may be related temporally, be part of an ensemble, or unrelated. Overall understanding and visualization of scientific processes require the study of individual fields and, more importantly, the development of methods to compare them meaningfully. In this thesis, we focus on the problem of designing meaningful measures to compare scalar fields by comparing their abstract representations called topological structures. We emphasize on intuitive and practical measures with useful properties and applications.

Motivation

Scalar fields are omnipresent when it comes to measuring and simulating scientific phenomena. Analysis and visualization of these scalar fields lead to a better understanding of the processes involved. Direct analysis and visualization of such a scalar function using standard visualization techniques like isosurface construction or volume rendering provides a good overview but is limited by two factors. First, increasing size of data makes storage and retrieval inefficient. Second, the analysis often requires a sweep over a large subset of the domain or range of the function even when the features of interest may be contained within a small region. These limitations are amplified when we consider time-varying scalar functions. Thus, these techniques are not well suited for feature directed analysis and visualization. This has necessitated the need for a summarized representation. This is and has been addressed by topological data structures. Topological structures provide us with an abstract representation of the scalar field, thus reducing the complexity while retaining the salient features. These structures have been successfully used in the recent years to represent scalar fields in a meaningful and succinct manner. Such representations have facilitated a feature-aware, interactive and exploratory analysis and visualization resulting in better understanding of these phenomena. Various topological data structures like persistence diagrams, merge trees, contour trees, Reeb graphs, extremum graphs, Morse-Smale complexes have been defined in the literature which provide meaningful combinatorial abstractions of the scalar field while capturing different aspects of the field. The properties of these structures have also been well-studied along with efficient algorithms to compute them.
Many of these scientific phenomena may vary with time resulting in a set of scalar fields that are related temporally. They may vary based on different parameters resulting in ensembles. They can also be just a set of scalar fields which are neither related temporally nor dependent on any parameters but still needs to be compared to understand the phenomena. Overall understanding may mandate not just studying the individual fields but also methods to study them together in a global context and compare them meaningfully. Such methods have been found useful for tracking features in time-varying phenomena, topological shape matching, detecting symmetry/asymmetry in scalar fields, or clustering, computing temporal summaries of large data sets, to identify features that are preserved in ensemble simulations or multi-field data, or to compare simulated data against measured data. This project deals with such methods which facilitate meaningful representations of time-varying fields and also comparative measures which compare topological structures which represent the scalar fields.

Problem

Designing comparison measures to facilitate meaningful comparisons of scalar functions through topological structures which are abstract and combinatorial representations. Along with these measures we aim to prove some theoretical properties of these measures, provide implementations which are efficient, and showcase their utility in various applications.

Comparison pipeline

We describe a typical comparison pipeline (Figure 1). The pipeline starts with scalar fields - individual, time-varying or ensembles - constructs topological structures as their abstract representations, compare the topological structures using a comparison measure customised for such comparison or the application, and finally provides an output which captures the similarity/dissimilarity of the fields which can be used further to gain insights about the underlying scalar fields and drive applications mentioned in the previous section. We illustrate the comparison pipeline with an example. Symmetry detection in bio-molecules is an important application which helps the biologists to understand the structure and function of the molecules. The measurements are typically done by Cryo-electron microscopy (Cryo-EM) which provides electron density - a scalar field - corresponding to the bio-molecule. In this case since the biologists are interested in similar substructures present within the same molecule, the field should be compared to itself. The field will contain noise and also point-wise comparison won’t lead to meaningful comparisons of the high level structures which the biologists would be interested in. To remove noise and also get an abstraction which captures such structures we build a topological structure like a split tree out of the scalar field and remove topological noise via simplification. We then compare the tree to itself using some local comparison measure to build a distance matrix. The sub-matrices provides us the symmetric structures in multiple scales.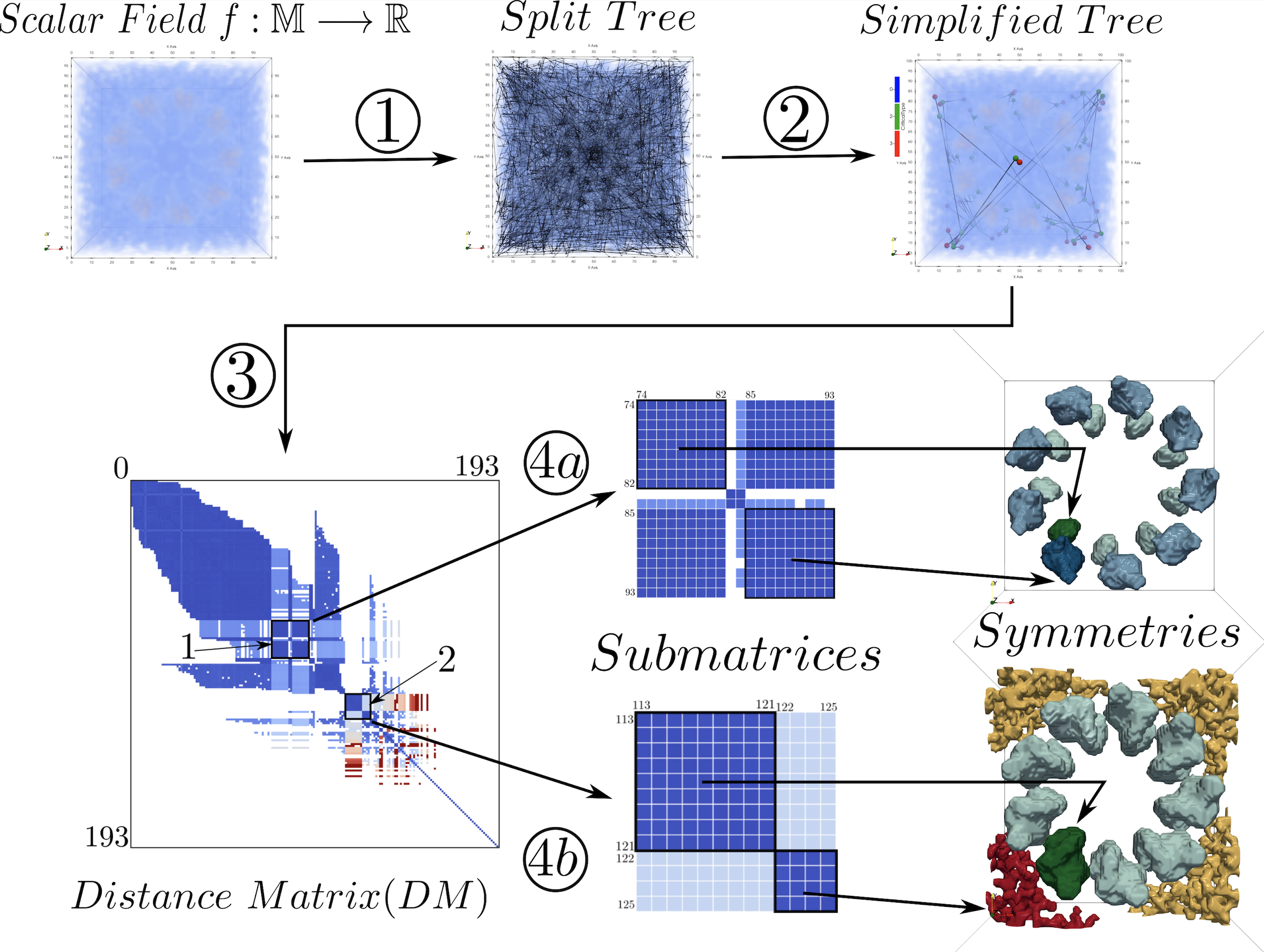



Illustrating a typical comparison pipeline. The pipeline takes a scalar field as the input, in step 1 it computes the topological structure, a split tree, in step 2 the tree is simplified by removing topological noise, in step 3 the simplified tree is compared to itself to generate a distance matrix DM, in step 4 the sub-matrices correspond to the symmetric regions which can be used to extract them as shown in the bottom right.

We give an overview of the our contribution to facilitate comparison – local and global – of various topological structures.

Global comparison of merge trees OTED, MTED

We start with global comparison of merge trees. Merge trees capture the topology of the sub-level/super-level sets to provide a succinct representation of the scalar fields.
We adapt the ordered tree edit distance from Xu assuming merge trees to be ordered rooted binary trees to design OTED [1]. The important contributions include,

• A simple comparison measure for merge trees.
• A simple cost model based on topological persistence.
• Applications to periodicity detection and symmetry detection in 2D scalar fields.

Continuing the work on merge trees, we alleviate the shortcomings of OTED, we adapt the constrained tree edit distance for unordered rooted trees by Zhang to merge trees with significant modifications and propose MTED [2]. The important contributions include,

• An intuitive and mathematically sound cost model for the individual edit operations.
• A proof that the comparison measure is a metric under the proposed cost model.
• A computational solution to handle instabilities.
• Experiments to demonstrate the utility of the distance measure
• Periodicity detection in 2D time-varying data.
• Temporal summarization to support visualization of 3D time-varying data.
• Symmetry detection in scalar fields.
• Study of topological effects of subsampling and smoothing.
• Shape matching.

Local comparison of merge trees LMTED

While global comparison measures like OTED and MTED help to address variety of interesting problems, they do not support fine-grained and hierarchical analysis of local structures or substructures of scalar fields. We adapt MTED [2] with significant modifications to propose a local comparison measure called LMTED [4]. The important contributions include,

• A novel local tree edit distance (LMTED) to compare substructures in scalar fields.
• A proof that it satisfies metric properties.
• A dynamic programming algorithm to compute the LMTED efficiently.
• A notion of truncated persistence to compute costs of matching / correspondences, which brings in the additional benefit of saving computation time by reducing the number of comparisons.
• Experiments to demonstrate the practical value of the distance
• Symmetry detection at multiple scales.
• Analysis of the effects of smoothing and subsampling.
• Fine grained analysis of topological compression.
• Applications to feature tracking.

Publications

1. Raghavendra Sridharamurthy, Adhitya Kamakshidasan and Vijay Natarajan.
   Edit distances for comparing merge trees.
   
2. Raghavendra Sridharamurthy, Talha Bin Masood, Adhitya Kamakshidasan and Vijay Natarajan.
   Edit distance between merge trees.
   
3. Lin Yan, Talha Bin Masood, Raghavendra Sridharamurthy, Farhan Rasheed, Vijay Natarajan, Ingrid Hotz and Bei Wang.
   Scalar Field Comparison with Topological Descriptors: Properties and Applications for Scientific Visualization
   
4. Raghavendra Sridharamurthy and Vijay Natarajan.
   Comparative Analysis of Merge Trees using Local Tree Edit Distance
   

Contact

raghavendrag [at] iisc [dot] ac [dot] in.