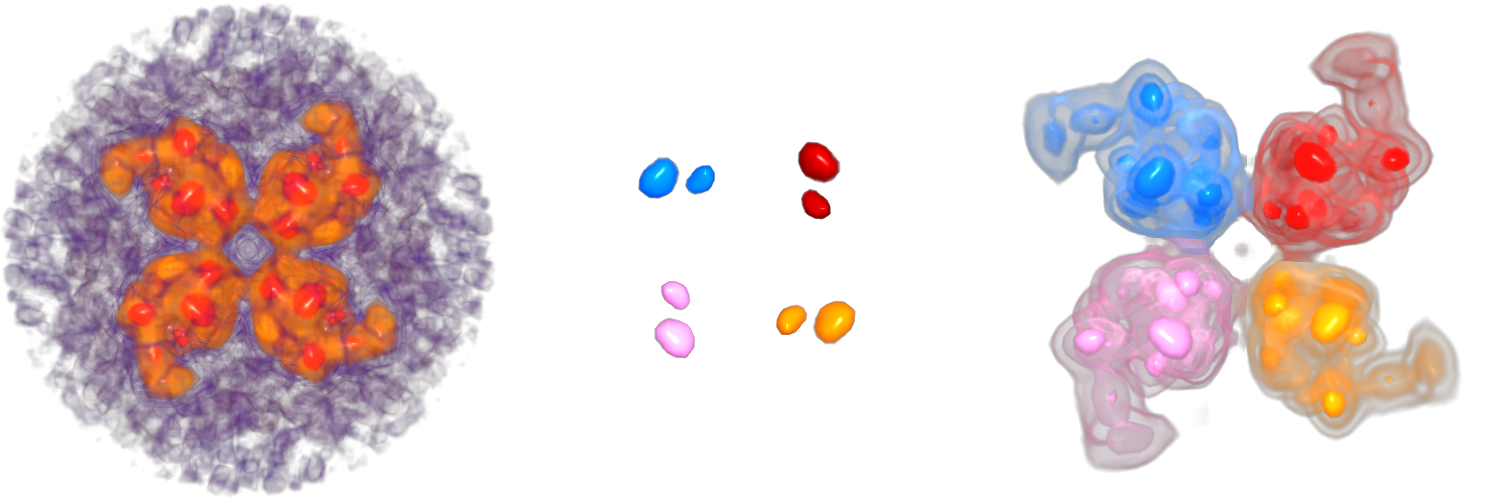Symmetry in Scalar Fields
People involved: Dilip Thomas and Talha Bin Masood
A scalar field is a real valued function defined on a domain of interest. Scalar field data
may be generated from experimental and computational methods in different disciplines
and are used to represent physical quantities measured over a domain of interest.
Study of symmetric or repeating
patterns in scalar fields is important in scientific data analysis because it gives deep insights
into the properties of the underlying phenomenon. The top row of Figure 1
shows three examples of symmetry in scalar fields. We study the problem of
detecting symmetric or repeating patterns in scalar fields and its applications to feature exploration and
visualization of scalar fields. The bottom row of Figure 1 shows the symmetric regions extracted
using the solutions we propose.
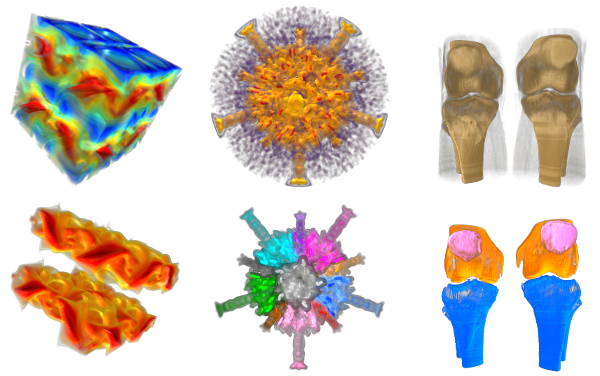 Figure 1. Symmetry is ubiquitous in scientific data sets as seen in the volume rendered images of
(top left) the temperature distribution in a Taylor-Green vortex flow simulation, (top center) a
cryo-electron microscopy image of a virus, and (top right) a CT scan image of a pair of knees.
While human beings are endowed with special cognitive ability that makes symmetry detection easy,
automatic detection of symmetry is a challenging task for computers. We propose algorithms
to identify symmetry and show different applications that exploit symmetry information to improve
visualization and exploration of scalar field data. Symmetry-aware transfer function highlights the
symmetric regions detected by (bottom left) identifying similar subtrees of the contour tree,
(bottom center) comparing distances between extrema using extremum graph, and (bottom right) clustering
contours in a high dimensional shape descriptor space.
Figure 1. Symmetry is ubiquitous in scientific data sets as seen in the volume rendered images of
(top left) the temperature distribution in a Taylor-Green vortex flow simulation, (top center) a
cryo-electron microscopy image of a virus, and (top right) a CT scan image of a pair of knees.
While human beings are endowed with special cognitive ability that makes symmetry detection easy,
automatic detection of symmetry is a challenging task for computers. We propose algorithms
to identify symmetry and show different applications that exploit symmetry information to improve
visualization and exploration of scalar field data. Symmetry-aware transfer function highlights the
symmetric regions detected by (bottom left) identifying similar subtrees of the contour tree,
(bottom center) comparing distances between extrema using extremum graph, and (bottom right) clustering
contours in a high dimensional shape descriptor space.
Motivation and Overview of Results
Human beings have special cognitive abilities that make it easy to recognize
symmetric patterns but it is a tough task for a machine to do so. Automatic detection
of symmetry is a challenging problem because both the segmentation of the domain
into potential symmetric segments and the correspondence between segments that are
symmetric need to be determined. Moreover, real life data sets never exhibit perfect
symmetry. This introduces additional challenges in determining symmetry in an approximate
sense as well as handling noise and missing parts within symmetric regions in the
data. Since the search space for locating symmetric segments is quite large, it is also
important to design an algorithm that is computationally efficient. Domain experts are interested
in studying important features that provide insights
about the underlying scientific phenomena that is being analyzed. Therefore, it
is pertinent for a scalar field symmetry detection algorithm to report symmetric segments
in a feature-aware manner.
We propose four methods to detect symmetry in scalar fields. The first
method models symmetry detection as a subtree matching problem in the contour tree,
which is a topological graph abstraction of the scalar field. The contour tree induces a
hierarchical segmentation of features at different scales and hence this method can detect
symmetry at different scales. The second method identifies symmetry by comparing dis-
tances between extrema from each symmetric region. The distance is computed robustly
using a topological abstraction called the extremum graph. Hence, this method can de-
tect symmetry even in the presence of significant noise. The above methods compare
pairs of regions to identify symmetry instead of grouping the entire set of symmetric
regions as a cluster. This motivates the third and fourth methods which uses a clustering analysis
for symmetry detection. In the third method, the contours of a scalar field are mapped to
points in a high-dimensional shape descriptor space such that points corresponding to similar
contours lie in close proximity to each other. Symmetry is identified by clustering the
points in the descriptor space. In the fourth method, pairs of points which are locally symmetric
vote for geometric transformations and symmetry transformation is identified as clusters in the space
of all transformations.
Symmetry Detection by Identifying Similar Subtrees in Contour Trees
The first method [1] models symmetry detection as a subtree matching problem
in the contour tree, which is a topological graph abstraction of the scalar field.
We propose a comparison measure for identifying similar subtrees of a contour tree
based on a topological measure called persistence. This leads to an algorithm that
detects symmetry by classifying subtrees of the contour tree into different groups.
Regions of the domain corresponding to subtrees that belong to a common group
are extracted and reported to be symmetric. Since the contour tree induces a hierarchical
segmentation of features at different scales, this method can detect symmetry at different scales.
Figure 2 shows an illustration of this method. A volume rendering of a cryo-electron microscopy image of
RuBisCO molecule in complex with RuBisCO large subunit methyltransferase
(EMDB 1734) highlights the symmetric or repeating patterns in the scalar field.
Our algorithm classifies subtrees of the contour tree
into different groups based on similarity. Subtrees that belong
to the same group are shown with the same color.
We extract regions of the domain corresponding to subtrees that belong to
the same group and report them to be symmetric.
Four different
groups of symmetric regions identified by our algorithm are shown in cyan, magenta, brown, and
violet.
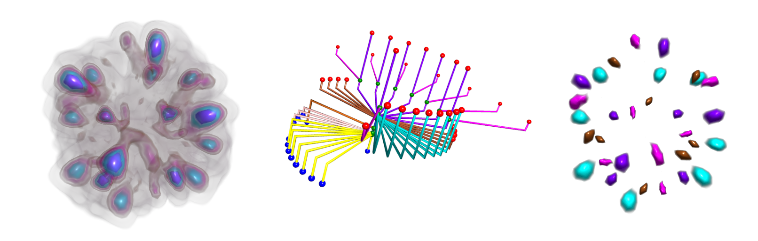 Figure 2. Symmetric patterns identified using the contour tree
in a cryo-electron microscopy image of RuBisCO
molecule in complex with RuBisCO large subunit methyltransferase (EMDB 1734).
(left) Volume rendering of the molecule highlight repeating structures in the scalar field.
(center) The contour tree for the data set.
Subtrees of the contour tree are classified into different groups based on similarity. Subtrees belonging
to a common group are shown with the same color.
(right) Four different types of regions, indicative of the different subunits in the molecule, identified by the symmetry detection algorithm
shown in cyan, magenta, brown, and violet. Regions with the same color are symmetric.
Figure 2. Symmetric patterns identified using the contour tree
in a cryo-electron microscopy image of RuBisCO
molecule in complex with RuBisCO large subunit methyltransferase (EMDB 1734).
(left) Volume rendering of the molecule highlight repeating structures in the scalar field.
(center) The contour tree for the data set.
Subtrees of the contour tree are classified into different groups based on similarity. Subtrees belonging
to a common group are shown with the same color.
(right) Four different types of regions, indicative of the different subunits in the molecule, identified by the symmetry detection algorithm
shown in cyan, magenta, brown, and violet. Regions with the same color are symmetric.
Symmetry Detection by Distance Comparison using Extremum Graphs
The second method we propose identifies symmetry by comparing distances between extrema
from each symmetric region [2]. We propose a data structure called the augmented extremum
graph and use it to design an algorithm for robust estimation of distances. The augmented
extremum graph captures both topological and geometric information of the scalar field
and enables robust and computationally efficient detection of symmetry. We show through
experiments on different cryo-electron microscopy datasets that the algorithm is capable of
detecting symmetry even in the presence of significant noise.
Figure 3 shows 4-fold rotational symmetry in the cryo-electron microscopy (cryo-EM)
data of Rubisco RbcL8-RbcX2-8 complex (EMDB 1654).
We perform Morse decomposition
of the data and select a set of Morse cells as
seed cells. The augmented extremum graph is traversed to compute distances from the seed cells to the remaining
Morse cells and merge the seed cells into super-seeds.
Eight seeds cells are selected for this data set
and they merge to form four super-seeds as shown in the center. The four
super-seeds provide an initial estimate of the 4-fold symmetry in the data which is then expanded in a region growing
stage. The 4-fold symmetry in the data thus identified is shown on the right.
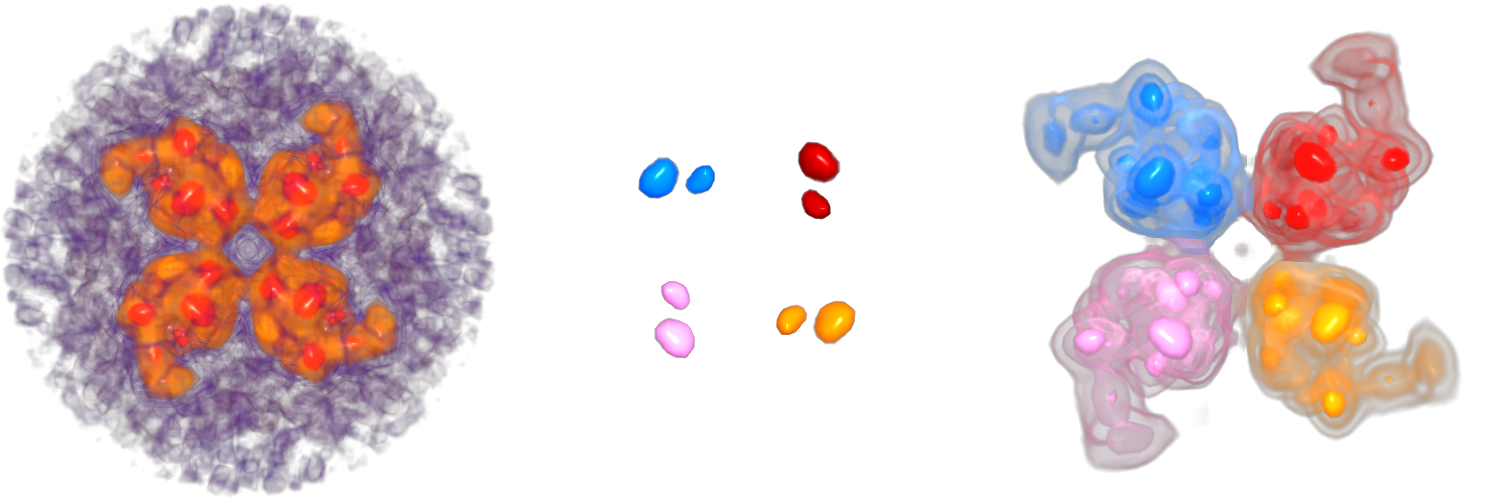 Figure 3. Symmetry identification algorithm based on
augmented extremum graph detects symmetry even in the presence of significant noise
in the electron microscopy data of the Rubisco RbcL8-RbcX2-8 complex (EMDB 1654). (left) Volume rendering
shows symmetry and noise in the data. (center) A set of seed cells is chosen as source vertices for traversing
the augmented extremum graph of the data. During the traversal, the seed cells merge together to form four
symmetric super-seeds. Seed cells that belong to a common super-seed are shown with the same color.
(right) The initial estimate of symmetry is expanded in a region growing stage to identify the symmetric regions.
A symmetry-aware transfer function highlights the 4-fold rotational symmetry detected in the Rubisco complex.
Figure 3. Symmetry identification algorithm based on
augmented extremum graph detects symmetry even in the presence of significant noise
in the electron microscopy data of the Rubisco RbcL8-RbcX2-8 complex (EMDB 1654). (left) Volume rendering
shows symmetry and noise in the data. (center) A set of seed cells is chosen as source vertices for traversing
the augmented extremum graph of the data. During the traversal, the seed cells merge together to form four
symmetric super-seeds. Seed cells that belong to a common super-seed are shown with the same color.
(right) The initial estimate of symmetry is expanded in a region growing stage to identify the symmetric regions.
A symmetry-aware transfer function highlights the 4-fold rotational symmetry detected in the Rubisco complex.
Symmetry Detection by Clustering Contours
The study of symmetry detection in shapes have established that
clustering based analysis result in superior performance and robust identification of
symmetry. Such an analysis avoids the need for comparing pairs of regions to identify symmetry and can
instead group a set of symmetric regions as a cluster. This motivates the third method which uses a clustering analysis
for symmetry detection [3]. In this method, we present a
novel representation of contours with the aim of studying the similarity relationship between the contours.
The representation maps contours to points in a high-dimensional transformation-invariant shape descriptor space.
We leverage the power of this representation to design a clustering based algorithm for detecting symmetric
regions in a scalar field. By selecting
a contour from each arc of the contour tree, we are able to detect symmetry at different scales similar
to the contour tree based approach. Noise in the
data is seamlessly handled by the clustering framework through the choice of a robust shape descriptor. Thus, our approach
combines the advantages of the earlier methods based
on the contour tree and extremum graph.
Figure 4 illustrates our approach on a 3D cryo-EM image of AMP-activated kinase (EMDB-1897)
with three-fold rotational symmetry. The large-scale features shown in gold and the small-scale features shown in blue and pink
highlight the multiscale aspect of our approach.
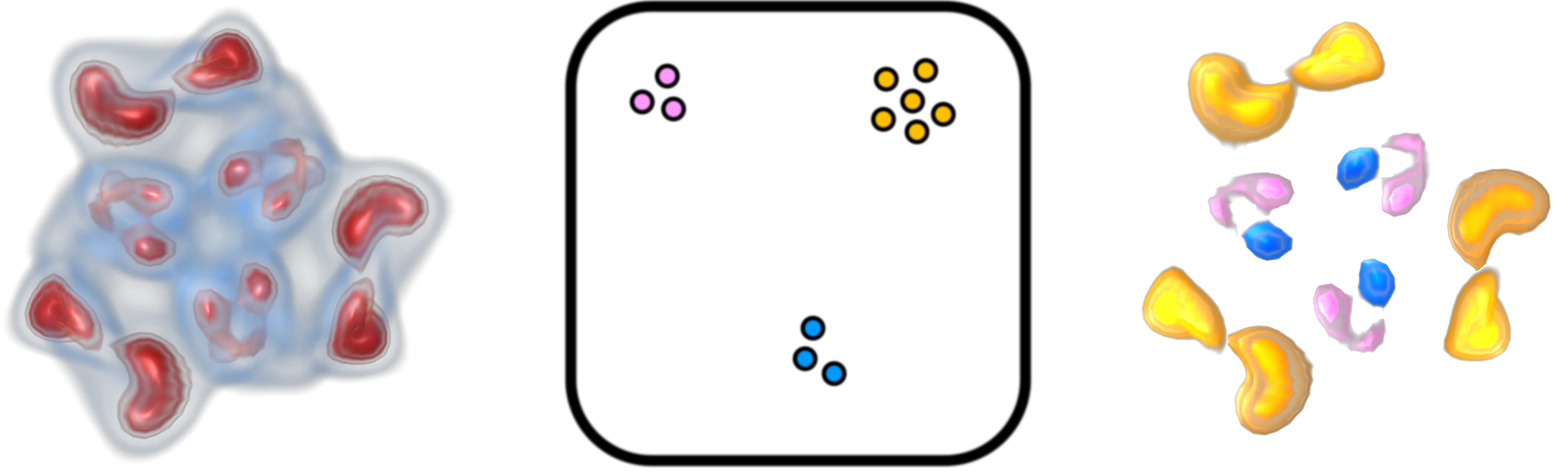 Figure 4. Clustering based analysis detects symmetry at different scales
in a 3D cryo-electron microscopy image of AMP-activated kinase (EMDB-1897).
(left) The three-fold rotational symmetry is apparent from the volume rendering. (center) Contours
are represented as points in a high-dimensional shape descriptor space (illustrated in 2D).
Symmetric contours form a cluster in the descriptor space and can be easily identified.
Three such clusters are shown in gold, blue, and pink. (right) Three symmetric regions of
different sizes, highlighted in gold, blue, and pink, detected by the method.
Figure 4. Clustering based analysis detects symmetry at different scales
in a 3D cryo-electron microscopy image of AMP-activated kinase (EMDB-1897).
(left) The three-fold rotational symmetry is apparent from the volume rendering. (center) Contours
are represented as points in a high-dimensional shape descriptor space (illustrated in 2D).
Symmetric contours form a cluster in the descriptor space and can be easily identified.
Three such clusters are shown in gold, blue, and pink. (right) Three symmetric regions of
different sizes, highlighted in gold, blue, and pink, detected by the method.
Symmetry Detection by Clustering Point Pairs
In this method [4], points are sampled from the domain and for each sample point a descriptor that captures the
scalar field locally is computed. The descriptor consists of an invariant component and an
alignment component. The invariant component of a point consists of properties of the
field like scalar value, gradient magnitude, and curvature of the level set passing through
the point. The alignment component of a point consists of vectors like the gradient vector
and the principal curvature directions of the level set passing through the point. These
vectors are used to define a local coordinate frame at each point. Sample points with
similar invariant components are paired together and the transformation that maps the
points in the pair is computed using their local coordinate frame. Since the scalar field
is locally similar for the points in a pair, they are considered to be locally symmetric.
Each pair then votes for the symmetry transformation that maps the points in the pair
in the space of all transformations. Symmetry detection problem is then reduced to
finding clusters in the high-dimensional transformation space. Each cluster corresponds
to aggregation of votes for a particular symmetry transformation. These clusters are
identified using a clustering technique. Finally, the symmetry transformation is spatially
verified and the symmetric regions are extracted and reported. An illustration of this
technique on a synthetic 2D scalar field data set is shown in Figure 5.
 Figure 5. Illustration of symmetry detection by clustering point pairs on a synthetic
data set. (left) The input scalar field. (left-centre) Points sampled from the domain shown in green.
(centre) The sample points corresponding to the endpoints of each line segment are locally
similar and hence paired together. For each pair, the transformation that maps the points
in the pair is represented as a point in a transformation space. (right-centre) The clusters in the
transformation space are identified. (right) For each cluster, the corresponding symmetry
transformation is spatially verified and the symmetric regions, shown in red and blue,
are extracted.
Figure 5. Illustration of symmetry detection by clustering point pairs on a synthetic
data set. (left) The input scalar field. (left-centre) Points sampled from the domain shown in green.
(centre) The sample points corresponding to the endpoints of each line segment are locally
similar and hence paired together. For each pair, the transformation that maps the points
in the pair is represented as a point in a transformation space. (right-centre) The clusters in the
transformation space are identified. (right) For each cluster, the corresponding symmetry
transformation is spatially verified and the symmetric regions, shown in red and blue,
are extracted.
Applications
Visualizing symmetric or repeating patterns
in the data often help the domain scientists in understanding and characterizing the features in
the data. We design novel applications that use symmetry information to facilitate visualization and exploration
of scalar field data. Some of the applications we propose like symmetry-aware transfer function design,
symmetry-aware isosurface extraction, and symmetry-aware editing and rendering enhance traditional visualization methods.
In addition, we also propose applications like query driven exploration, asymmetry visualization, and
proximity-aware visualization that can significantly aid users in the analysis and exploration of scalar fields.
We believe that the methods we propose for symmetry detection will open new frontiers in analyzing structural
similarity of scalar fields and more applications of symmetry detection will emerge.
Publications
- Dilip Mathew Thomas and Vijay Natarajan.
Symmetry in scalar field topology.
- Dilip Mathew Thomas and Vijay Natarajan.
Detecting symmetry in scalar fields using augmented extremum graphs.
- Dilip Mathew Thomas and Vijay Natarajan.
Multiscale symmetry detection in scalar fields by clustering contours.
- Talha Bin Masood, Dilip Mathew Thomas and Vijay Natarajan.
Scalar field visualization via extraction of symmetric structures.
Software
-
SymmteryViewer
A web-server for symmetry computation within EMDB data.
Contact
Contact dilthoms [at] gmail [dot] com for the software.