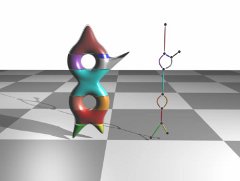
Constructing Reeb graphs using cylinder maps.

Harish Doraiswamy, Aneesh Sood, and Vijay Natarajan.
SoCG 2010: ACM Symposium on Computational Geometry, Video / Multimedia track, 2010.

Abstract

The Reeb graph of a scalar function represents the evolution of the topology of its level sets. In this video, we describe a near-optimal output-sensitive algorithm for computing the Reeb graph of scalar functions defined over manifolds. Key to the simplicity and efficiency of the algorithm is an alternate definition of the Reeb graph that considers equivalence classes of level sets instead of individual level sets. The algorithm works in two steps. The first step locates all critical points of the function in the domain. Arcs in the Reeb graph are computed in the second step using a simple search procedure that works on a small subset of the domain that corresponds to a pair of critical points. The algorithm is also able to handle non-manifold domains.

[PDF]

---

Supplementary Material:

1. Constructing Reeb Graphs using Cylinder Maps - A video illustration (Download) This video illustrates the two-step algorithm for computing the Reeb graph of a piecewise-linear (PL) function using Cylinder maps.