Efficient algorithms for computing Reeb graphs.

Harish Doraiswamy and Vijay Natarajan.
Computational Geometry: Theory and Applications, 42, 2009, 606-616.
[Elsevier link]

Abstract

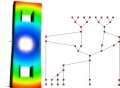
The Reeb graph tracks topology changes in level sets of a scalar function and finds applications in scientific visualization and geometric modeling. We describe an algorithm that constructs the Reeb graph of a Morse function defined on a 3-manifold. Our algorithm maintains connected components of the two dimensional levels sets as a dynamic graph and constructs the Reeb graph in O(n log n+n log g(log log g)³) time, where n is the number of triangles in the tetrahedral mesh representing the 3-manifold and g is the maximum genus over all level sets of the function. We extend this algorithm to construct Reeb graphs of d-manifolds in O(n log n(log log n)³) time, where n is the number of triangles in the simplicial complex that represents the d-manifold. Our result is a significant improvement over the previously known O(n²) algorithm. Finally, we present experimental results of our implementation and demonstrate that, in practice, our algorithm for 3-manifolds performs better than what the theoretical bound suggests.

[PDF]